BLOG

16 Dec 2019
Having a custom sized base is useful for security purposes, as it obscures whatever string of digits you put into it. It’s also handy for making long numbers much shorter and thus take up less space. We will be using base 62, comprised of the digits 0-9, the uppercase letters A-Z, and the lowercase letters a-z.
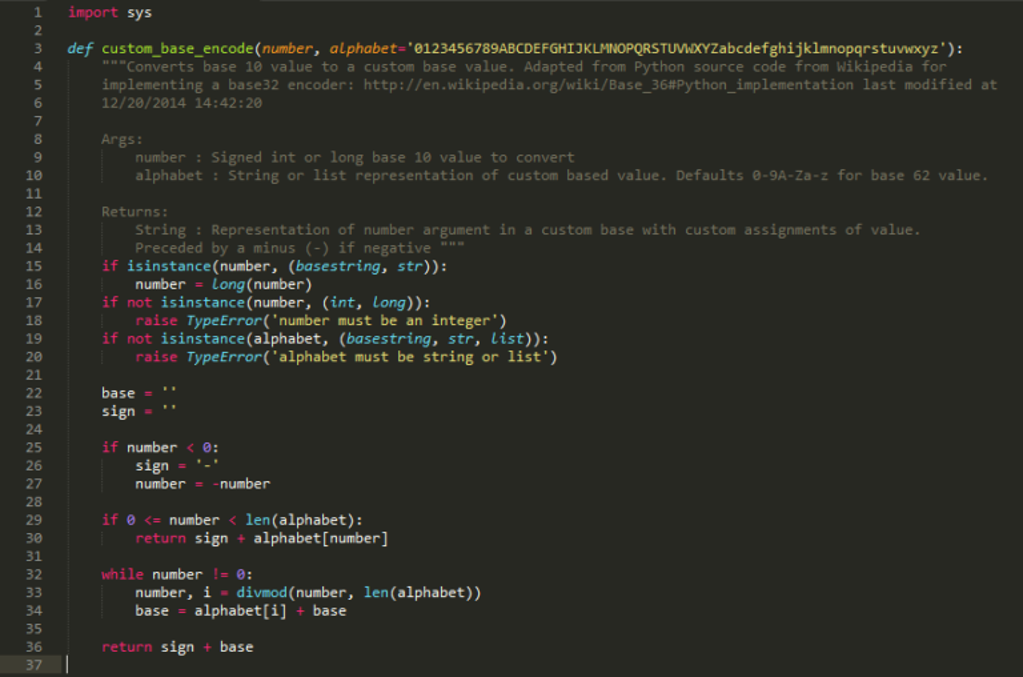
If you are having difficulties reading any of the code, click on any image to see a larger version. The code is adapted from this source: http://en.wikipedia.org/wiki.Base_36#Python_implementation.
Line 3 defines the Python function for custom base system. So long as each character included for the argument “alphabet” here is unique, this can be as long or short as you want it to be.

Lines 15 to 20 are some basic type checks to ensure that the input argument is valid for performing the rest of the code. Python is not a strongly-typed language, meaning that there are not compile-time checks and will attempt to run code even if it is invalid. These steps tell Python when the input is invalid, and the return message is set to explain the problem, i.e. entering a value which is not an integer or a list into the respective fields.
Lines 25 to 30 ensure that any negative numbers are returned as negatives after the conversion, though their value is temporarily made positive in order to assign the correct value.
The code on lines 32 to 34 are what wraps the number around to make sure it increases to the correct columns. Just as the decimal number 10 has a 1 in the 10 column and a 0 in the 1 column, 100 in base 62 reads as 1 in the 62 column and c in the 1 column. So, 100 in base 62 returns the value 1c.
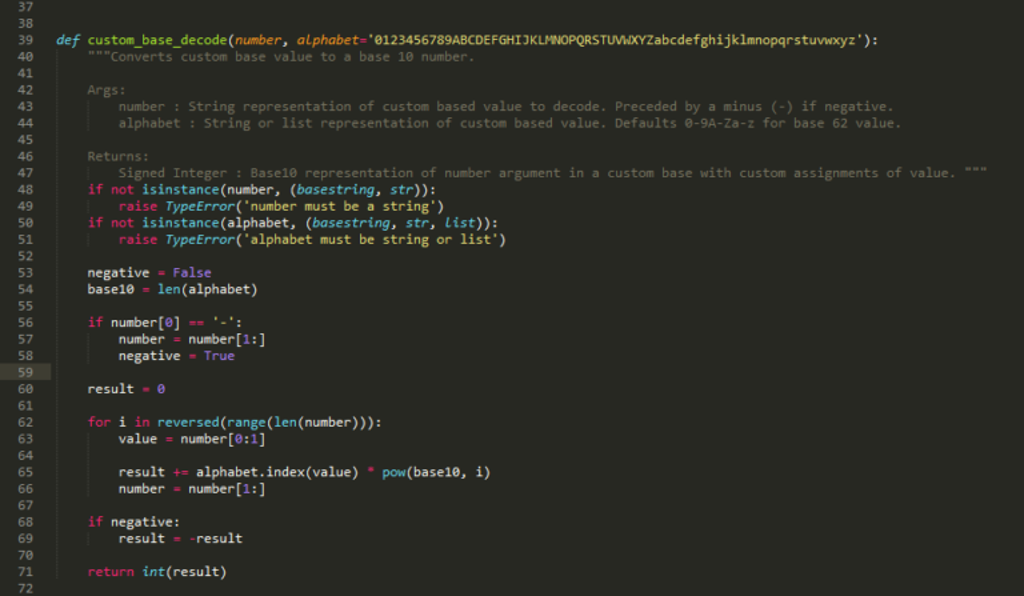
When taken as a whole, this function will covert any number into a base 62 string. The code below then reverse this, translating a custom base value (base 62 if not specified) number back to its original base 10.
This part of the code is mostly just inverting the steps outlined above. To ensure that the decoding produces the correct result, the alphabet must match the one used within your initial encoding. Again, the setup is ensuring the function arguments are valid, and then determining whether the input number is negative.
Lines 62 exists to make sure the code resolves in the correct order. We find the length of the number, find the range from 0 – in the case of the number ‘1c’ in hexadecimal, the range will be 0 to 1. The order is reversed as we will be reading from left to right, and the left-most number has the highest value. The variable ‘i’ denotes which column we are currently looking at when converting back to base 10. Lines 68 to 69 then make sure that any negative number is correctly restored to its negative value.
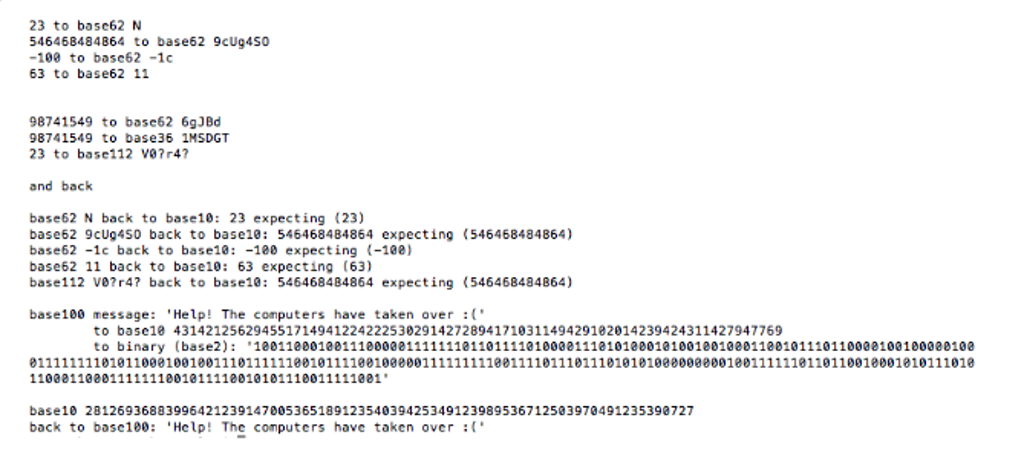
Below that, we have also included some examples of how different numbers look when run through this script.
To further encrypt and strengthen the protections of these custom base numbers, it is possible to store numbers in a different base again. Lines 86 and 94 refer to changing the outputted base 62 value into a hexadecimal number, thus adding an extra layer of protection to it. This could be repeated any number of times with different bases to further obscure the true value of the number that was originally inputted.
The only limiting factor in base size is the number of unique characters available in whichever encoding you are using. Theoretically, once you start including things like Chinese and Japanese characters, you have an incredibly vast base number. In fact, Unicode 9.0 has a total of 128,172 characters, meaning that a number can easily be represented as base 128172 values.
Obviously, if you are hoping to obscure values then base 128172 would be a fairly feasible and straight-forward method of doing so. For example, first converting a string using ASCII encoding to an integer, then converting that base 10 number to a base 128172 value would be simple. The more times you do this with different alphabets, the more confused your result would appear. As long as the decoding is performed in the reverse order you will retrieve the original value.
One usage for base changing would be for a referral code generator for a system’s users. If a system contains a list of users, all with numeric IDs, the system owner wouldn’t want to publicise the private IDs used to reference these users. However, if the number base was changed from a base 10 to a base 36 (0 to 9 and uppercase A to Z, in a random order) then without knowing the decoding order, the referral code will seem like a random unique ID.